PERCEPATAN PADA MOMEN INERSIA

Perbandingan Percepatan Momen Inersia pada Bola Pejal, Bola Berongga, Silinder Pejal, dan Cincin  Diasumsikan \[\theta = 90^\circ, \quad g = 10 \, \text{m/s}^2\] BOLA PEJAL \[a = \frac{F}{\left(\frac{I}{r^2} + m\right)} = \frac{F}{\left(\frac{\frac{2}{5}mr^2}{r^2} + m\right)} = \frac{m g \sin \theta}{\frac{2}{5}m + m} = \frac{g \sin \theta}{\frac{7}{5}} = \frac{5 g \sin(90^\circ)}{7} = \frac{5 \cdot 10 \cdot 1}{7} = 7.14 \, \text{m/s}^2\] BOLA BERONGGA \[a = \frac{F}{\left(\frac{I}{r^2} + m\right)} = \frac{F}{\left(\frac{\frac{2}{3}mr^2}{r^2} + m\right)} = \frac{m g \sin \theta}{\frac{2}{3}m + m} = \frac{g \sin \theta}{\frac{5}{3}} = \frac{3 g\sin(90^\circ)}{5} = \frac{3 \cdot 10 \cdot 1}{5} = 6 \, \text{m/s}^2\] CINCIN \[a = \frac{F}{\left(\frac{I}{r^2} + m\right)} = \frac{F}{\left(\frac{mr^2}{r^2} + m\right)} = \frac{m g \sin \theta}{m + m} = \frac{g \sin \theta}{2} = \frac{g \sin(90^\circ)}{2} = \frac{10 \cdot 1}{2} = 5 \, \text{m/s}^2\] SILINDER PEJAL \[a = \frac{F}{\left(\frac...
1 komentar

BENDA TEGAR

Benda Tegar dalam Fisika

Benda tegar adalah konsep penting dalam fisika yang membahas tentang objek yang mempertahankan bentuk dan kekekalan relatifnya terhadap gaya yang bekerja padanya. Dalam fisika, benda tegar adalah benda yang tidak mengalami perubahan bentuk atau deformasi saat dikenai gaya eksternal.Secara sederhana, benda tegar bisa berupa balok, lingkaran, silinder, atau objek lain yang tidak mengalami perubahan struktural saat diberi gaya. Ini berbeda dengan benda yang tidak tegar (benda deformabel), seperti karet atau plastik, yang dapat berubah bentuk saat diberi gaya dan kembali ke bentuk semula setelah gaya tersebut dihilangkan.

Pengertian Benda Tegar

Benda tegar merupakan objek yang tidak mengalami deformasi atau perubahan bentuk ketika dikenai gaya eksternal. Dalam fisika, benda tegar sering digunakan untuk menggambarkan objek yang stabil secara bentuk.

 Sifat-Sifat Benda Tegar

 -Kekakuan Benda Tegar:

  Benda tegar memiliki sifat kekakuan yang membuatnya tidak mengalami perubahan bentuk.

 -Rotasi dan Translasi:

  Benda tegar dapat bergerak dalam dua cara, yaitu rotasi (berputar) dan translasi (bergerak maju mundur).

 -Titik Tumpu dan Sumbu Rotasi:

  Pada benda tegar, rotasi terjadi sekitar sumbu tertentu atau titik tumpu.

 


Rumus-Rumus Terkait Benda Tegar

 1.Moment Gaya (Torsi/Torque):

   \[ \tau = F \times r \times \sin(\theta) \]

   dengan:

   - \(\tau\) adalah moment gaya.

   - \(F\) adalah gaya yang diterapkan.

   - \(r\) adalah jarak antara sumbu putar dan garis aksi gaya.

   - \(\theta\) adalah sudut antara vektor gaya dan vektor jarak.

 

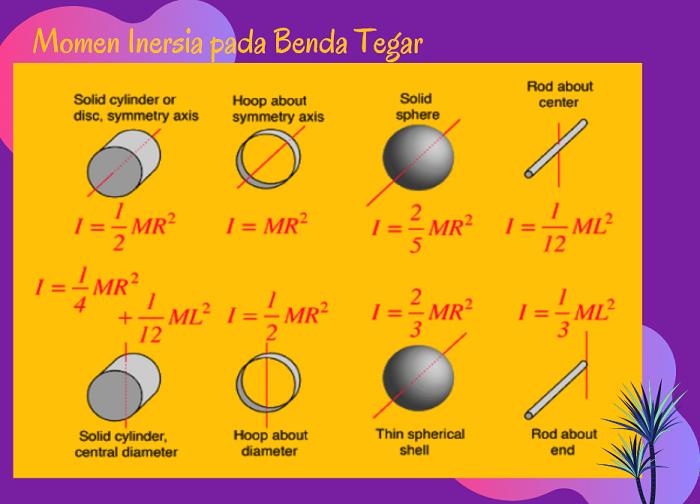
2.Moment Inersia (Inertia):

   - Untuk benda silinder: \( I = \frac{1}{2} m r^2 \)

   - Untuk benda bola: \( I = \frac{2}{5} m r^2 \)

   - Untuk benda persegi panjang: \( I = \frac{1}{3} m l^2 \)

   dengan:

   - \(I\) adalah moment inersia.

   - \(m\) adalah massa benda.

   - \(r\) atau \(l\) adalah jari-jari atau panjang benda.

 

Contoh Soal 

Contoh Soal 1:

Sebuah benda silinder dengan massa \(4 \, \text{kg}\) dan jari-jari \(0.6 \, \text{m}\) berputar mengelilingi ujungnya. Hitunglah moment inersia benda tersebut terhadap sumbu putarnya.

Pembahasan Contoh Soal 1:

Untuk mencari moment inersia (\(I\)) sebuah silinder terhadap sumbu putarnya, kita menggunakan rumus moment inersia untuk benda silinder yang merupakan \(I = \frac{1}{2} m r^2\).

Diketahui:

- Massa silinder (\(m\)) = \(4 \, \text{kg}\)

- Jari-jari silinder (\(r\)) = \(0.6 \, \text{m}\)

 Substitusi nilai-nilai tersebut ke dalam rumus moment inersia untuk silinder:

\[ I = \frac{1}{2} m r^2 \]

\[ I = \frac{1}{2} \times 4 \, \text{kg} \times (0.6 \, \text{m})^2 \]

\[ I = \frac{1}{2} \times 4 \times 0.36 \]

\[ I = 0.5 \times 0.36 \]

\[ I = 0.18 \, \text{kg} \, \text{m}^2 \]

 

Jadi, moment inersia benda silinder tersebut terhadap sumbu putarnya adalah \(0.18 \, \text{kg} \, \text{m}^2\).

 

Contoh Soal 2:

Sebuah gaya \(15 \, \text{N}\) diterapkan pada jarak \(0.4 \, \text{m}\) dari sumbu putar pada benda silinder. Jika sudut antara vektor gaya dan vektor jarak adalah \(45^\circ\), berapa besar moment gaya yang dihasilkan?

Pembahasan Contoh Soal 2:

Kita akan menggunakan rumus moment gaya (\(\tau = F \times r \times \sin(\theta)\)) untuk menghitung moment gaya yang dihasilkan. 

Diketahui:

- Besar gaya (\(F\)) = \(15 \, \text{N}\)

- Jarak dari sumbu putar (\(r\)) = \(0.4 \, \text{m}\)

- Sudut antara vektor gaya dan vektor jarak (\(\theta\)) = \(45^\circ\)

 

Substitusi nilai-nilai tersebut ke dalam rumus moment gaya:

 

\[ \tau = F \times r \times \sin(\theta) \]

\[ \tau = 15 \, \text{N} \times 0.4 \, \text{m} \times \sin(45^\circ) \]

\[ \tau = 15 \times 0.4 \times \frac{\sqrt{2}}{2} \]

\[ \tau = 6 \sqrt{2} \]

\[ \tau \approx 8.49 \, \text{Nm} \]

 

Jadi, moment gaya yang dihasilkan adalah sekitar \(8.49 \, \text{Nm}\).

 

Kesimpulan:

Pemahaman tentang benda tegar sangat penting dalam fisika, terutama dalam memahami rotasi, torsi, dan pergerakan benda dalam keadaan tertentu. Dengan memahami rumus dan konsep-konsep terkait benda tegar, kita dapat menerapkannya dalam pemecahan masalah fisika yang kompleks.


Referensi

Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics. Wiley.

Serway, R. A., & Jewett, J. W. (2017). Physics for Scientists and Engineers with Modern Physics. Cengage Learning.

Knight, R. D. (2016). Physics for Scientists and Engineers: A Strategic Approach with Modern Physics. Pearson.

Giancoli, D. C. (2014). Physics: Principles with Applications. Pearson.

 

Komentar

Posting Komentar

Postingan populer dari blog ini

GAYA SENTRAL

Mengenal Lebih Dalam Tentang Gaya Sentral dalam Fisika  Gaya sentral merupakan salah satu konsep penting dalam fisika yang mendeskripsikan gaya yang bekerja pada suatu benda dan selalu menuju atau menjauh dari titik tertentu yang tetap, seperti titik pusat. Gaya ini bergantung pada jarak antara objek yang dikenai gaya dengan titik pusatnya. Konsep Gaya Sentral Definisi Gaya Sentral Gaya sentral adalah gaya yang memiliki arah yang selalu menuju atau menjauh dari sebuah titik tetap, dengan besaran yang tergantung pada jarak antara objek yang dikenai gaya dengan titik pusatnya. Representasi Matematis Gaya sentral sering dinyatakan dengan persamaan: \[ F = k \cdot r^n \] di mana: - \( F \) adalah gaya sentral. - \( k \) adalah konstanta proporsional. - \( r \) adalah jarak antara objek dan titik pusat. - \( n \) adalah eksponen yang menentukan tipe dari gaya sentral (misalnya, \( n = -1 \) untuk gaya gravitasi dan \( n = 2 \) untuk gaya coulomb).   Ru...
Read more »

SIFAT DAN KARAKTERISTIK GELOMBANG

    GELOMBANG      Pengertian/Defenisi      Gelombang adalah perambatan atau propagasi energi atau gangguan melalui medium atau ruang kosong. Ini adalah konsep yang luas dan penting dalam berbagai bidang ilmu, termasuk fisika, teknik, dan ilmu alam. Gelombang dapat ditemukan dalam berbagai bentuk, termasuk gelombang mekanik seperti gelombang air dan gelombang suara, serta gelombang elektromagnetik seperti cahaya dan gelombang radio. Sifat-sifat Gelombang 1. Amplitudo (A)      Amplitudo gelombang adalah tinggi maksimum atau "kekuatan" gelombang. Semakin besar amplitudo, semakin besar energi yang dibawa oleh gelombang tersebut. 2. Panjang Gelombang (λ)      Panjang gelombang adalah jarak antara dua puncak berturut-turut atau lembah berturut-turut dalam gelombang. Panjang gelombang ini dapat bervariasi tergantung pada jenis gelombangnya 3. Frekuensi (f)    Frekuensi gelombang adalah jumlah getaran atau siklus g...
Read more »